【物理基礎】力学1
公式解説
v=\frac{x}{t}速さ❲m/s❳=\frac{距離❲m❳}{時間❲s❳}速さとは1秒あたりに進む距離のことです。
速度とは速さに向きを加えた量のことです。
速さは定義なので暗記必須です。
公式解説
x=vt
距離❲m❳=速さ❲m/s❳×時間❲s❳
等速直線運動とは、一定の速さで直進する運動です。
速さを時間で積分すると距離を導出できます。
\begin{align*}
x &= \int v\, dt \\
&=vt
\end{align*}
公式解説
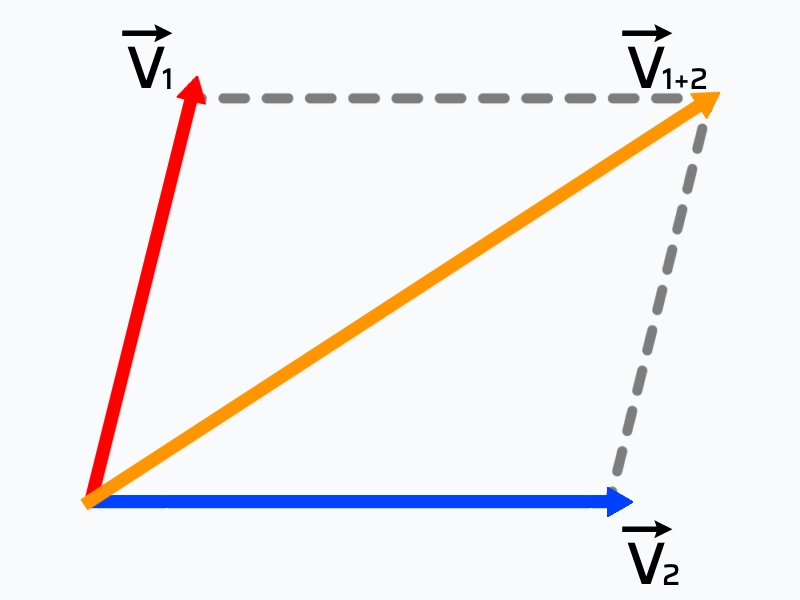
\overrightarrow{v}_Aと\overrightarrow{v}_Bの合成は\\⠀\\\overrightarrow{v}_A+\overrightarrow{v}_B\overrightarrow{速度}_Aと\overrightarrow{速度}_Bの合成は\\⠀\\\overrightarrow{速度}_A+\overrightarrow{速度}_B合成速度とは複数の速度が組み合わさって生じる速度のことです。
速度はベクトルなので、図で表すと導出できます。
公式解説
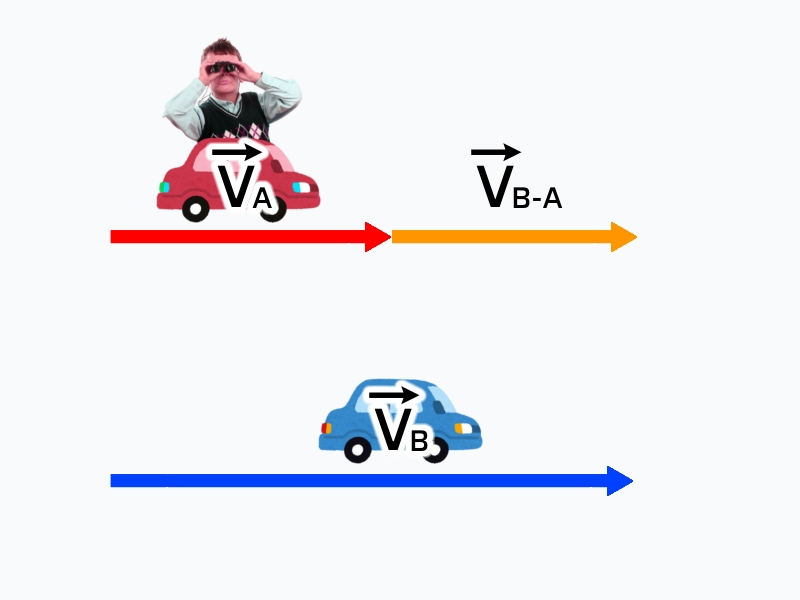
\overrightarrow{v}_Aから見た\overrightarrow{v}_Bの相対速度は\\⠀\\\overrightarrow{v}_B-\overrightarrow{v}_A\overrightarrow{速度}_Aから見た\overrightarrow{速度}_Bの相対速度は\\⠀\\\overrightarrow{速度}_B-\overrightarrow{速度}_A相対速度とは、観測者から見た対象の速度のことです。
対象の速度から観測者の速度を引くと覚えましょう。
これもベクトルで書くと導出できます。
公式解説
v=v_0+at
速さ❲m/s❳=初速度❲m/s❳+加速度❲m/s^2❳×時間❲s❳
等加速度運動とは、加速度が常に一定である運動のことです。
加速度とは、単位時間に速度が変化する割合(傾き)です。
等加速度運動は、速度–時間グラフで導出できます。
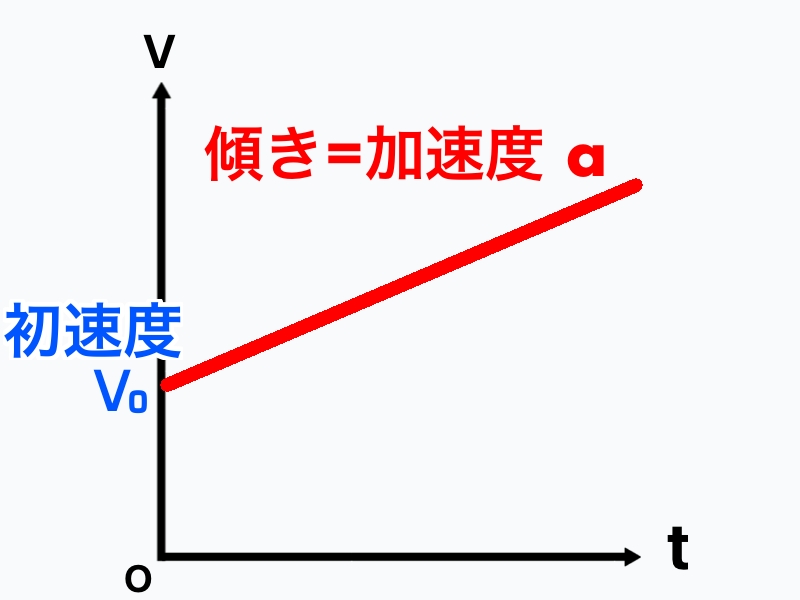
切片が初速度 v_0\\⠀\\傾きが加速度 a より\\⠀\\v=v_0+at
公式解説
x=v_0t+\frac{1}{2}at^2距離❲m❳=初速度❲m/s^2❳×時間❲s❳+\frac{1}{2}×加速度❲m/s^2❳×時間❲s❳^2上の速度-時間グラフの面積が移動距離になります。
速さを時間で積分すると距離を導出できます。
\begin{align*}
x &= \int v\, dt \\
&= \int (v_0 + a t)\, dt \\
&= v_0 t + \frac{1}{2} a t^2
\end{align*}
公式解説
v^2-v_0^2=2ax
速さ❲m/s❳^2-初速度❲m/s❳^2=2×加速度❲m/s^2❳×距離❲m❳
等加速度運動で、時間 t を使わずに速度と移動距離を結びつける式です。
上の二つの公式からtを削除して導出できます。
\begin{align*}
v &= v_0 + a t \\
x &= v_0 t + \frac{1}{2} a t^2 \\⠀\\
\text{(時間 } t &\text{を消去すると)}\\⠀\\\quad v^2 - v_0^2 &= 2 a x
\end{align*}

